Question

Without using the property of parallel lines, prove that in a parallelogram each pair of consecutive angles are supplementary.

Answer 1

The definition of parallelogram is that both pairs of opposing sides are parallel. However, they have other properties:

0. Both pairs of opposite sides are congruent.

,

1. Both pairs of opposite angles are congruent.

,

2. Diagonals bisect each other.

,

3. One pair of opposite sides are congruent AND parallel.

Based on the properties of parallelograms, we know that ∠A is congruent to ∠C. Therefore if we divide the figure into two triangles as follows, m∠A will be divided into two.

As m∠A is the same as m∠C, then when dividing them by two, the final answer will be the same. For example, if m∠A = 60°, m∠C = 60° , then:

`(m\angle C)/(2)+(m\angle A)/(2)=(60)/(2)+(60)/(2)=30+30=60`

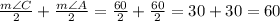
Then, as the measure of the interior angles of a triangle is equal to 180°, then:

`m\angle D=180-(m\angle C)/(2)-(m\angle A)/(2)`

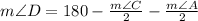
Based on the latter, we can conclude that one angle is supplementary to both consecutive angles.