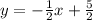Question

Writing the equation of a line through the two given points of (-3, 4) and (3, 1)

Answer 1

The form of the equation of the line is

`y=mx+b`

Where m is the slope and b is the y-intercept

In order to find the equation of the line first, we need to find the slope using the next formula

`m=(y_2-y_1)/(x_2-x_1)`

where m is the slope, (x1,y1) and (x2,y2) are points where the line passes through

in our case

(-3,4)=(x1,y1)

(3,1)=(x2,y2)

we substitute the values

`m=(1-4)/(3+3)=(-3)/(6)=-(1)/(2)`

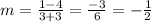
Then we need to find the y-intercept so we will use the form of the line we will use x=3 and y=1

`1=-(1)/(2)(3)+b`

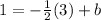
then we isolate the b

`b=1+(3)/(2)=(5)/(2)`

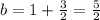
ANSWER

The equation of the line is

`y=-(1)/(2)x+(5)/(2)`