Question

The height (perpendicular line segment) of an isosceles triangle from a vertex to the base is 4 inch long.If the base of this triangle is 6 inch long, how long will the legs of this triangle be (in inches)?

Answer 1

Given:

Height of the isosceles triangle = 4 inches

Base of triangle = 6 inches

Let's find the length of the legs of the traingle.

Let's sketch a figure which represents this isosceles triangle.

Since the triangle is an isoceles triangle, the length of the legs will be equal.

a = b

To find the length of the legs, apply Pythagorean Theorem:

`c^2=a^2+b^2`

Where:

a = 4 in

b = 3 in

Thus, we have:

`\begin{gathered} c^2=4^2+3^2 \\ \\ c^2=16+9 \\ \\ c^2=25 \end{gathered}`

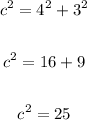
Take the square root of both sides:

`\begin{gathered} \sqrt[]{c}^2=\sqrt[]{25}^2 \\ \\ c=5 \end{gathered}`

Therefore, the length of the legs of the isosceles triangle is 5 inches.