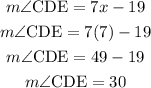Let's draw the figure:
CDE is the exterior angle to the Triangle BCD.
The two opposite interior to CDE is the angle B and angle C.
We know:
An exterior angle of a triangle is equal to the sum of the two opposite interior angles.
Thus, we can write
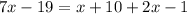
Now, let's solve for x:
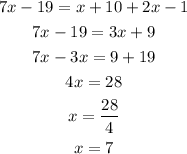
We want to find the angle CDE. Thus,