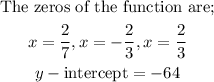Question

Find the zeros and y intercept equation is on the photo

Answer 1

Given the function;

`g(x)=2(7x-2)^3(4-9x^2)`

To find the zeros of this function, we shall set the function equal to zero and solve for the variable x. This is shown below;

`\begin{gathered} \text{We start by factorizing the right side of the function;} \\ 2(7x-2)^3(4-9x^2) \\ =2(7x-2)^3(-9x^2+4) \\ \text{Factor out -1 and you'll have;} \\ =2(7x-2)^3-1(9x^2-4) \\ =2(7x-2)^3-1(3x+2)(3x-2) \\ =-2(7x-2)^3(3x+2)(3x-2) \end{gathered}`

We now have;

`-2(7x-2)^3(3x+2)(3x-2)=0`

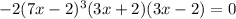
Next we'll apply the zero factor principle which states that;

`\begin{gathered} If \\ ab=0 \\ \text{Then,} \\ a=0,\text{ or b}=0 \end{gathered}`

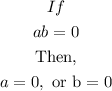
We will now have the following;

`\begin{gathered} 7x-2=0 \\ 7x=2 \\ x=(2)/(7) \end{gathered}`
`\begin{gathered} 3x+2=0 \\ 3x=-2 \\ x=-(2)/(3) \end{gathered}`
`\begin{gathered} 3x-2=0 \\ 3x=2 \\ x=(2)/(3) \end{gathered}`

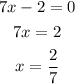
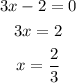
To calculate the y-intercept, we simply find the value of the equation when x = 0.

We'll now have the following;

`\begin{gathered} y=2(7x-2)^3(4-9x^2) \\ y=2(7\lbrack0\rbrack-2)^3(4-9\lbrack0\rbrack^2) \\ y=2(0-2)^3(4-0) \\ y=2(-2)^3(4) \\ y=2(-8)(4) \\ y=-64 \end{gathered}`

ANSWER:

`\begin{gathered} \text{The zeros of the function are;} \\ x=(2)/(7),x=-(2)/(3),x=(2)/(3) \\ y-\text{intercept}=-64 \end{gathered}`