Evaluate the product of matrix A and matrix B to obtain the matrix AB.
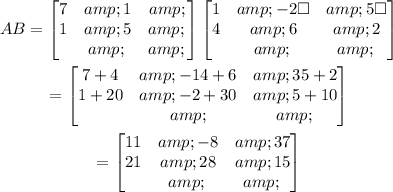
Evalaute the product of AB matrix with C matrix to obtain matrix for (AB)C.

Evalaute the product of matrix B and matric C to obtain the matrix BC,
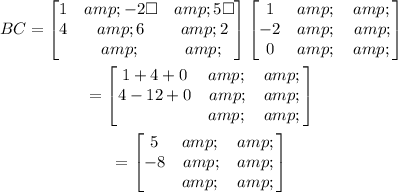
Evaluate the product of matrix A with matrix (BC) to obtain the matrix A(BC).
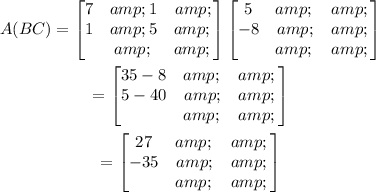
So it can be observed that A(BC) = (AB)C.