Question

Find the vertex and write the quadratic function in vertex form (which our OpenStax textbook also calls the standard form).f(x)=x^2−12 x + 136 Give the vertex. Enter your answer as a point (a,b).Vertex: Preview Enter the coordinates of the vertex to write f(x) in vertex form:f(x)=(x− )2+

Answer 1

In an equation in the form:

`f(x)=ax^2+bx+c`

The x-coordinate of the vertex is given by the next formula:

`x=-(b)/(2a)`

And the y coordinate of the vertex y the value of f in that x.

For the given function:

`f(x)=x^2-12x+136`

x-coordinate of the vertex:

`x=-((-12))/(2(1))=(12)/(2)=6`

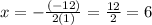
y-coordinate of the vertex:

`\begin{gathered} f(6)=(6)^2-12(6)+136 \\ f(6)=36-72+136 \\ f(6)=100 \end{gathered}`

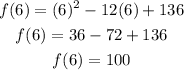
Vertex: (6,100)

Vertex form of a quadratic function:

`\begin{gathered} f(x)=a(x-h)^2+k \\ \\ \text{Vertex: (h,k)} \end{gathered}`

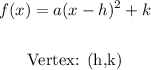
For the given function the vertex form is:

`f(x)=(x-6)^2+100`

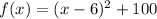
Graph with the vertex: