Question

Justin's truck was totaled and he needs a new one, but cannot afford it with the money he has in the bank. so he gets a 13.5% per year. How much interest will be charged in the first 10 months? How much will he owe after 10 months assuming he did not make any payments?

Answer 1

The compound interest formula is:

`A=P(1+(r)/(n))^(nt)`

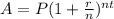
Where

P is principal

r is rate of interest

n is number of compounding

t is number of years

Putting the given information, we have:

`\begin{gathered} A=P(1+(r)/(n))^(nt) \\ A=13,500(1+(0.135)/(12))^(12) \\ A=13500(1.01125)^(12) \\ A=15439.60 \end{gathered}`

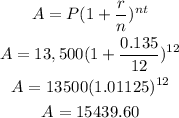
Interest amount is:

15,439.60 - 13,500 = $1939.60 (in a year/12 months)

In 10 months:

`1939.60*(10)/(12)=1616.33`

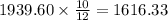
Justin would owe $1616.33 after 10 months.