Question

According to Masterfoods, the company that manufactures M&M’s, 12% of peanut M&M’s are brown, 15% are yellow, 12% are red, 23% are blue, 23% are orange and 15% are green. (Round all answers to 3 places after the decimal point, if necessary.)(a) Compute the probability that a randomly selected peanut M&M is not green.P(not green) = (b) Compute the probability that a randomly selected peanut M&M is orange or brown.P(orange or brown) = Compute the probability that two randomly selected peanut M&M’s are both green.P(both green) =(d) If you randomly select six peanut M&M’s, compute that probability that none of them are red.P(none are red) =e) If you randomly select six peanut M&M’s, compute that probability that at least one of them is red.P(at least one is red) =

Answer 1

The percetnts of the M&M's are:

12% brown

15% yellow

12% red

23% blue

23% orange

15% green

a) The probability of selecting a random peanut not green is all the other percent but the green one:

`P(not\text{ }green)=(100-15)/(100)=0.85`

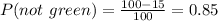
Then the probability is 0.85

b) The probability of selecting a random peanut orange or brown is the percent of both colors added:

`P(orange\text{ }or\text{ }brown)=(23+12)/(100)=0.35`

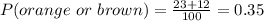
Then the probability is 0.35

For the next questions, we will assume a population of 100, 100 peanuts. It would make easier the analysis.

c) If you got 100 peanuts and you know that 15 of them are green, then the probability of both peanuts being green, we need to multiplicate the probability of the two events, like this:

`P(one\text{ }green)* P(one\text{ }green\text{ }after\text{ }first\text{ }selection\text{ })=(15)/(100)*(14)/(99)=(7)/(330)`

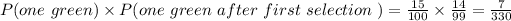
Remember that these events are dependent events.

Then the probability is 7/330.

d) The same thing that in c) but with six peanuts, and having in mind the probability of selecting a none red peanut:

`P(none\text{ are red})\text{ }=(88)/(100)*(87)/(99)*(86)/(98)*(85)/(97)*(84)/(96)*(83)/(95)=0.455`

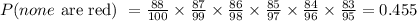
Then the probability is 0.455

e) Again it is a dependent event, so we use the same analysis that the points before, but with one change. We need to determine the probability of the selecting peanut would be red and multiplicate it by 6 because there be 6 attempts.

`P(at\text{ least one is red})\text{ }=(12)/(100)*6=0.72`

Then the probability is 0.72