Question

The following equations represent part of a radioactive decay series: Fill in the table with the correct particle or element, and describe the types of radiation given off in the series.

Answer 1

Step 1 - How to discover the missing particles or elements

In a chemical or physical process, three properties of matter must always be conserved: energy, mass and electrical charge. We can use this conservation to discover the missing particle in the given equations.

Since we know that the mass must be the same, we can call x the mass of the particle C in the first equation. The atomic number above each element is a measure of the number of protons and, indirectly, a measure of positive charges. Since the charge must also be the same in both sides of the equation, let's set the atomic number of particle C as y.

We can rewrite equation 1 thus as:

`^(238)_(92)U\rightarrow^y_xC+^4_2He_{}`

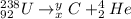
But because the mass and the charge must be conserved, we have that:

`\begin{gathered} 238=4+y\rightarrow y=234 \\ \\ 92=2+x\rightarrow x=90 \end{gathered}`

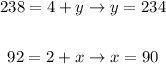
Therefore, the correct particle produced in equation 1 is:

`^(234)_(90)C`

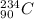
To discover which element was formed, we can look at a periodic table. Remember that what defines an element is the atomic number, which is 90, in this case. The element that was formed is thus Th. The full equation 1 becomes:

`^(238)_(92)U\rightarrow^(234)_(90)Th+^4_2He_{}`

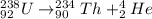
Step 2 - Following the same procedure to solve the remaining equations

We can work in the same way with equation 2. Let's say x is the mass of particle F and y is its atomic number. Therefore:

`^(234)_(90)Th\rightarrow^(234)_(91)Pa+^y_xF`

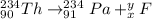
By the conservation of both mass and electrical charge:

`\begin{gathered} 234=234+y\rightarrow y=0 \\ \\ 90=91+x\rightarrow x=-1 \end{gathered}`

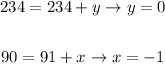
The particle F is thus:

`^0_(-1)F`

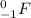
We can see the atomic number is 0, i.e., there are no protons, and the charge is -1. This particle corresponds thus to an electron. Full equation 2 becomes:

`^(234)_(90)Th\rightarrow^(234)_(91)Pa+^0_(-1)e`

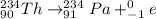
Step 3 - Naming the radioactive process

There are three main radioactive processes:

Alpha: an Hellium nucleus is liberated

Beta: an electron is liberated

Gamma: only radiation, i.e., no particles are liberated

We can see that, in equation 1, we have formed a nucleus of Hellium. Therefore, equation 1 corresponds to an alpha decay.

Equation 2, on the other hand, has liberated an electron. Therefore, equation 2 corrresponds to a beta decay.