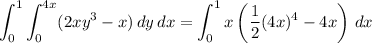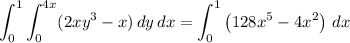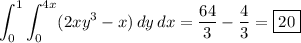Question

Evaluate the line integral by the two following methods. Xy dx + x2y3 dy c is counterclockwise around the triangle with vertices (0, 0), (1, 0), and (1, 4).

Answer 1

Not sure what "two methods" you refer to, so I'll assume you're supposed to compute the line integral directly as well as with Green's theorem.

Direct computation:

It looks like the line integral is

`\displaystyle \int_C xy \, dx + x^2y^3 \, dy`

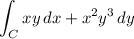
where C is the union of three line segment. We'll partition C and parameterize each component by

• C₁, the line segment from (0, 0) to (1, 0) : x(t) = t and y(t) = 0;

• C₂, from (1, 0) to (1, 4) : x(t) = 1 and y(t) = 4t;

• C₃, from (1, 4) to (0, 0) : x(t) = 1 - t and y(t) = 4 - 4t;

each with 0 ≤ t ≤ 1.

Compute the integrals over each component:

• Along C₁, we have y = 0, so this integral contributes nothing.

• Along C₂,

`\displaystyle \int_0^1 4t \cdot 0 \, dt + (4t)^3 \cdot 4 \, dt = 256 \int_0^1 t^3 \, dt = 64`

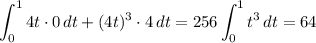
• Along C₃,

`\displaystyle \int_0^1 (1-t)(4-4t) \cdot (-dt) + (1-t)^2(4-4t)^3 \cdot (-4\, dt) \\\\ = \int_0^1 \left(-260 + 1288 t - 2564 t^2 + 2560 t^3 - 1280 t^4 +  256 t^5 \right) \, dt = -44`

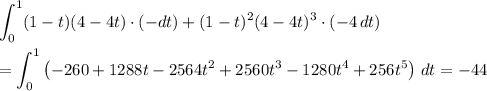
So, the total line integral is

`\displaystyle \int_C xy \, dx + x^2y^3 \, dy = 0 + 64 - 44 = \boxed{20}`

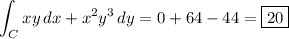
Using Green's theorem:

The interior of C is the triangular region

`D = \{(x, y) : 0 \le x \le 1 \text{ and } 0 \le y \le 4x\}`

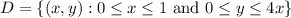
and the integrand has no singularities either on C or within D. So by Green's theorem,

`\displaystyle \int_C xy \, dx + x^2y^3 \, dy = \iint_D (\partial(x^2y^3))/(\partial x) - (\partial(xy))/(\partial y) \, dx \, dy = \int_0^1 \int_0^(4x) (2xy^3 - x) \, dy \, dx`

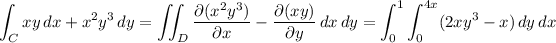
The remaining integral is trivial.

`\displaystyle \int_0^1 \int_0^(4x) (2xy^3 - x) \, dy \, dx = \int_0^1 x \int_0^(4x) (2y^3 - 1) \, dy \, dx`

`\displaystyle \int_0^1 \int_0^(4x) (2xy^3 - x) \, dy \, dx = \int_0^1 x \left(\frac12 (4x)^4 - 4x\right) \, dx`

`\displaystyle \int_0^1 \int_0^(4x) (2xy^3 - x) \, dy \, dx = \int_0^1 \left(128x^5 - 4x^2\right) \, dx`

`\displaystyle \int_0^1 \int_0^(4x) (2xy^3 - x) \, dy \, dx = \frac{64}3 - \frac43 = \boxed{20}`