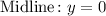1 Answer

Ian Samz · Answer 1 · 2023-04-01T06:14:01+0000

The general form of the cosine function is:

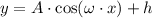
$y=A\cdot\cos (\omega\cdot x)+h$

Where A is the amplitude, ω is the angular frequency, and "h" is a translation factor.

We see that the function goes from -1 to +1 (y-coordinate). Then, the amplitude of the function is:

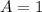
The period of the function is 2π. The period T relates to the angular frequency as:

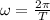
$\omega=(2\pi)/(T)$

From the value of T:

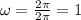
$\omega=(2\pi)/(2\pi)=1$

Finally, there is no vertical shift, so h must be 0. The final function is:

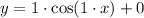
$y=1\cdot\cos (1\cdot x)+0$

Since the function is not shifted, the midline is just the x-axis:

$\text{Midline}\colon y=0$

Please log in or register to add a comment.