Question

Hello, pre calc question on functions. Thanks for your help!

Answer 1

From the graph, we can see that there is a hole at x=-2

`\begin{gathered} x=-2 \\ (x+2) \end{gathered}`

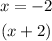
From the image below we have the vertical asymptotes to be

`\begin{gathered} x=3 \\ (x-3) \end{gathered}`

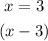
The x-intercepts or the zeros is given at

`\begin{gathered} x=2 \\ (x-2) \end{gathered}`

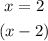
Hence,

The equation of the graph will be calculated below as

`g(x)=(a(x-2)(x+2))/((x-3)(x+2)_)`

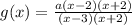
To find a, we will use the coordinates below

`(x,y)=(1,1)`
`\begin{gathered} g(x)=(a(x-2)(x+2))/((x-3)(x+2)) \\ 1=(a(1-2)(1+2))/((1-3)(1+2)) \\ 1=-(3a)/(-6) \\ 3a=6 \\ (3a)/(3)=(6)/(3) \\ a=2 \end{gathered}`

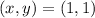
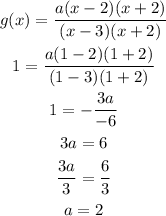
Hence,

The equation of g(x) will be

`\begin{gathered} g(x)=(2(x-2)(x+2))/((x-3)(x+2)) \\ g(x)=(2(x^2-4))/(x^2-x-6) \\ g(x)=(2x^2-8)/(x^2-x-6) \end{gathered}`

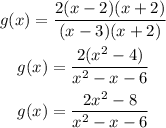
The final answer is

`\Rightarrow g(x)=(2x^(2)-8)/(x^(2)-x-6)`

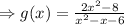
The SECOND OPTION is the right answer