Question

How much do you have to deposit today in order to have $5000 in two years?Assume the APR is 3% compounding quarterly.A. $625.00B. $4709.88C. $5307.99D. $4375.00

Answer 1

We are asked to find the principal for an amount compounded quarterly. Let's remember the formula for a future compounded quarterly:

`A=P(1+(r)/(4))^(4t)`

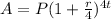
We solve for P:

`(A)/((1+(r)/(4))^(4t))=P`

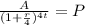
We are given the following values:

`\begin{gathered} A=5000 \\ r=0.03 \\ t=2 \end{gathered}`

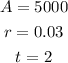
Replacing we get:

`(5000)/((1+(0.03)/(4))^((4)(2)))=P`

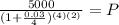
Solving the operations:

`4709.88=P`

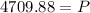
Therefore, the initial value must be $4709.88