A.
In order to calculate the cost of the two-line ad, let's use the value of x = 2 in the function, therefore let's choose the first part of the piecewise function:
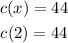
So the cost is $44
B.
Using x = 1 and x = 3, and then calculating the difference of c(1) and c(3), we have:
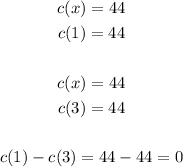
C.
Using x = 8, we need to use the second part of the piecewise function:
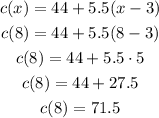
D.
Graphing the function, we have:
E.
The transition occurs at x = 3, and the cost is 44 at this point, so the coordinates are (3, 44).