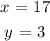From the given figure,
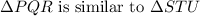
When two triangles are similar then ratio of their corresponding sides are similar.
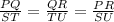
Substituting the values in the above equation,
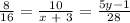
Calculating the value of x ,
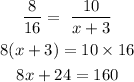
Rearranging the like terms o both the sides ,
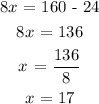
Calculating the value of y,
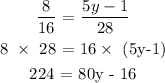
Rearranging the like terms on both the sides ,
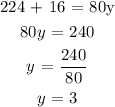
Thus the required values of x and y are ,