Question

Does x+2y=2(y-4)+2 represent a function?

Answer 1

x+2y=2(y-4)+2 doesnot represent a function

Step-by-step explanation:

`\begin{gathered} \text{Given:} \\ x+2y=2\mleft(y-4\mright)+2 \end{gathered}`

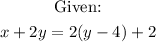
To determine if it is a function, first we need to simplify the equation:

`\begin{gathered} x\text{ + 2y = 2y - 8 + 2} \\ \text{collect like terms:} \\ x\text{ + 2y - 2y = -8 + 2} \\ x\text{ = -6} \\ \end{gathered}`

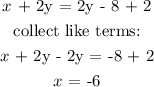
For a relation, to be a function, each of its input must have only one output

For x = -6, this gives a vertical line.

This shows that irrespective of the value of y, the x coordinate will remain the same.

Each input of x = -6, has more than one y values as the y values changes but the x value remains the same.

As a result, the given relation is not a function