Question

I need help with #9 It says to also round to the nearest hundredth. Please help!

Answer 1

452.39 cubic centimeters

Step-by-step explanation

the volume of a hemisphere is given by:

`V=(2)/(3)\pi r^3`

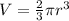
so

Step 1

find the radius:

the circumference is given by:

`C=2\pi r`

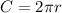
then, let

`C=37.7\text{ cm}`

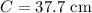
replace and solve for r

`\begin{gathered} C=2\pi r \\ r=(C)/(2\pi) \\ replace \\ r=\frac{37.7\text{ cm}}{2*3.14}=6 \\ r=6 \end{gathered}`

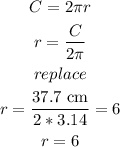
som the radius is 6 cm

Step 2

now, let

`r=6\text{ cm}`

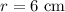
now, replace in the formula to find the volume of the hemisphere

`\begin{gathered} V=(2)/(3)\pi r^3 \\ V=(2)/(3)\pi(6\text{ cm\rparen}^3 \\ V=(2)/(3)\pi *216(\text{cm}^3) \\ V=452.3893\text{ \lparen cm}^3) \\ rounded \\ V=452.39\text{ \lparen cm}^3) \end{gathered}`

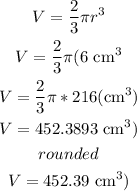
so, the answer is

452.39 cubic centimeters

I hope this helps you