Question

A tower casts a shadow that is 135 feet long. A person that is 5 ft - 3 in. casts a shadow that is 9 feet long. How tall is the tower?

Answer 1

The person and its shadow make a triangle, and the same happens with the building and its shadow. Those two triangles are similar, which means the ratio of the corresponding sides are equal.

Before calculating the ratios, let's write the person height only with one unit. The relation between feet and inches is

`\begin{gathered} 1ft=12in\text{.} \\ \Rightarrow3in.=0.25ft \end{gathered}`

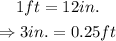
The height of the person is 5.25ft.

As I stated before, the ratio of the corresponding sides is equal because the triangles are similar, this means the ratio between the shadows is equal to the ratio between the heights. Let's call the height of the building as h

`(135)/(9)=(h)/(5.25)`

Solving for h

`\begin{gathered} (135)/(9)=(h)/(5.25) \\ h=5.25*(135)/(9)=5.25*15=78.75 \\ \end{gathered}`

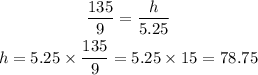
The height of the building is 78.75 ft.