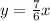Given that 'y' is directly proportional to 'x',
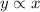
Let 'k' be the constant of proportionality.
Then the equation becomes,
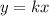
Given that 'y' is 14 when 'x' is 12,
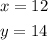
Substitute the values in the equation,
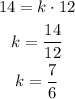
Substitute the value of 'k' in the equation,
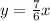
Thus, the required equation that relates 'x' and 'y' is,