Question

Which expression is equivalent to 3 square root of x to the power of 10

Answer 1

The trick of the problem is to change the question into: Which expression is equivalent to x^10? Because the 3 square root is not changed in any sense. Now, we need to remember what could be with an expression like x^10. First, one can't add numbers without care (sloppily). For instance, if our x were 1,

`x^(10)=(1)^(10)=1\\e3(1)=3\cdot x^(10)`

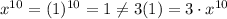
Thus, we must discard the second option. We can discard the third option too, for sum and product are really different operations. Finally, without discard the first option, I want to say that we can "separate" the exponent of an expression through the product. This could sound strange, but it just means

`x^(a+b)=x^a\cdot x^b`

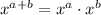
With this property in mind, we can say that

`x^(10)=x^(9+1)=x^9\cdot x^1=x^9\cdot x`

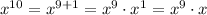
Thus, our answer is the last option.