0.6923
1) Gathering the data we have
Average: 23.7
Standard Deviation: 3
P < 24.7
2) We need to find out the z-score for P < 24.7. So we can write out the following. Plugging the X value for 24.7, the mean is 23.7, and the Standard Deviation: 3
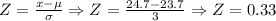
Now, with the Z-score table, we can locate the corresponding value:
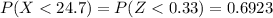
3) Hence, the probability that the lifetime of these phones will be less than 24.7 months is: 0.6923