Given the Exponential Function:

You know that it represents the amount A(t) of a sample of uranium-240 remaining (in grams) after "t" hours.
• Then, in order to calculate the amount of the sample remaining after 7 hours, you need to substitute this value into the function and evaluate:
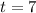
You get:

• In order to calculate the amount of the sample remaining after 40 hours, you need to substitute this value into the function and evaluate:
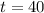
You get:
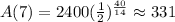
Hence, the answer is:
• Amount after 7 hours:
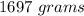
• Amount after 40 hours:
