Question

According to Wikipedia, as of November 1, 2021, 4,864 extrasolar planets have been identified. One of the closest multiple-planet solar systems to our own is around the star Gliese 876, about 15 light-years away, and it contains four planets. One takes 59.9 Earth days to revolve, at a distance of 3.18 x 107 kilometers from Gliese 876. Another planet takes 121 Earth days to revolve. How far is this second planet from Gliese 876? Include units in your answer. Answer must be in 3 significant digits.

Answer 1

According to the Kepler's Third Law of Planetary Motion, if the orbital period of an object around a body is T and the radius of the orbit is R, then, the quotient between the square of the period and the radius elevated to the third power is constant for any object in orbit around the same body:

`(T^2)/(R^3)=\text{constant}`

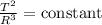
Let T₁ and R₁ represent the orbital period and the orbital radius of the first planet around Gliese 876, and let T₂ and R₂ represent the same magnitudes for the second planet. Then:

`(T^2_2)/(R^3_2)=(T^2_1)/(R^3_1)`

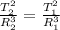
In the problem, R₂ is the unkown that we need to find. Isolate R₂ from the equation:

`\begin{gathered} \Rightarrow R^3_2=\mleft((T_2)/(T_1)\mright)^2R^3_1 \\ \Rightarrow R^{}_2=\mleft((T_2)/(T_1)\mright)^{(2)/(3)}R^{}_1 \end{gathered}`

To find the distance of the second planet to its star, substitute the values for the known variables: T₁=59.9 d, R₁=3.18*10^7 km, T₂=121 d:

Therefore, the second planet is 5.08*10^7 km away from its star, Gliese 876.