Question

A scientist has two solutions, which she has labeled Solution A and Solution B. Each contains salt. She knows that Solution A is 70% salt and Solution B is 95% salt. She wants to obtain 30 ounces of a mixture that is 90% salt. How many ounces of each solution should she use?Solution A:Solution B:

Answer 1

Solution A:6 ounces

Solution B: 24 ounces

Step-by-step explanation

Step 1

set the equations

let x represents the number of ounces fo solution A

let y represents the number of ounces fo solution B

Also

Solution A is 70% salt

Solution B is 95% salt

hence,

rewrite

a)She wants to obtain 30 ounces

`x+y=30\rightarrow equation(1)`

b) the final solution is 90% salt, hence

`\begin{gathered} 70\text{ \% of x +95\% of y= 90 \% of 30} \\ (70)/(100)x+(95)/(100)y=(90)/(100)30 \\ 0.7x+0.95y=27\rightarrow equation(2) \end{gathered}`

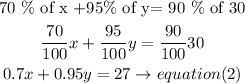
Step 2

solve the equations

a)isolate x in equation (1) and replace in equation(2)

so

`\begin{gathered} x+y=30\rightarrow equation(1) \\ \text{subtract x in both sides} \\ x+y-y=30-y \\ x=30-y\rightarrow equation\text{ (3)} \end{gathered}`

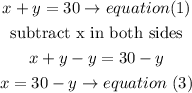
now,replace in equation (2)

`\begin{gathered} 0.7x+0.95y=27\rightarrow equation(2) \\ 0.7(30-y)+0.95y=27 \\ 21-0.7y+0.95y=27 \\ 21+0.25y=27 \\ \text{subtract 21 in both sides} \\ 21+0.25y-21=27-21 \\ 0.25y=6 \\ \text{divide both sides by 0.25} \\ (0.25y)/(0.25)=(6)/(0.25) \\ y=24 \end{gathered}`

therefore

Solution B: 24 ounces

b)now, replace the y value in equaiton (3)

`\begin{gathered} x=30-y\rightarrow equation\text{ (3)} \\ x=30-24 \\ x=6 \end{gathered}`

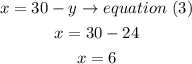
hence

Solution A:6 ounces

I hope this helps you