x=0.34
and
x=-4.34
Step-by-step explanationStep 1
given
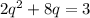
a)
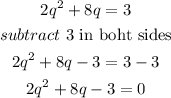
now,

Step 2
now,move
the constant to the right side by adding it on both sides

Take half of the q term and square it
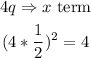
then add the result to both sides
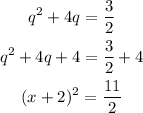
Step 3
finally, isolate x
![\begin{gathered} (x+2)^(2)=(11)/(2) \\ square\text{ root in both sides} \\ √((x+2)^2)=\sqrt{(11)/(2)} \\ x+2=\pm\sqrt{(11)/(2)} \\ subtract\text{ 2 in both sides} \\ x+2-2=\operatorname{\pm}\sqrt{(11)/(2)}-2 \\ x_1=\sqrt{(11)/(2)}-2=0.34 \\ x_2=-\sqrt{(11)/(2)}-2=-4.34 \end{gathered}]()
therefore, the solutions area
x=0.34
and
x=-4.34