Question

In an urn are 3 blue and 5 red balls.(a) Consider drawing with removing of 2 balls. What is the probability thati. only red balls are drawn?

Answer 1

Answer: 5/14

First, we list down all the possibilities of drawing the balls.

First, the probability of drawing a red ball on the first draw

Since there are 5 red balls and a total of 8 balls (3 blue + 5 red),

`P(1R)=(5)/(8)`

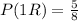
Since we remove the ball after drawing it, the next draw will have 4 red balls (after picking one) and a total of 7 balls

`P(2R)=(4)/(7)`

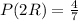
Then, to get the probability that only red balls are drawn, we will multiply the probabilities together::

`P(R)=(5)/(8)*(4)/(7)=(20)/(56)=(5)/(14)=0.3571=35.71\%`

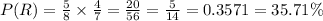
Therefore, the probability that only red balls are drawn is 5/14.