the cost of labour per hour is $7.20
the cost of raw materials per pound is $11.60
Step-by-step explanation:
For product one:
time = 5 hours of labour
let the cost labour per hour = x
Amount = 3 pounds of raw amterials
let the cost of one pound raw material = y
Cost to produce each product = $70.8
The equation:
time (cost per hour) + amount (cost of one pound of raw material) = Cost to produce each product
5(x) + 3(y) = 70.80
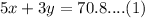
For product 2:
time = 3.5 hours of labour
let the cost of labour per hour = x
Amount = 13 pounds of raw amterials
let the cost of one pound raw material = y
Cost to produce each product = $176.00
The equation:
time (cost per hour) + amount (cost of one pound of raw material) = Cost to produce each product
3.5(x) + 13(y) = 176
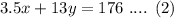
combining both equations:
5x + 3y = 70.8 ...(1)
3.5x + 13y = 176 ....(2)
Using elimination method:
To eliminate y, we will multiply equation (1) by 13 and equation (2) by 3 so that both coefficient of y become the same
65x + 39y = 920.4 ...(*1)
10.5x + 39y = 528 ...(2*)
subtract equation (2*) from (1*):
65x - 10.5x + 39y - 39y = 920.4 - 528
54.5x + 0 = 392.4
54.5x = 392.4
divide both sides by 54.5:
x = 392.4/54.5
x = 7.2
substitute for x in any of the equations
Using equation 1: 5x + 3y = 70.8
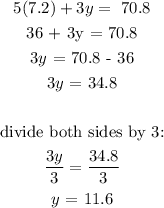
Hence, the cost of labour per hour is $7.20 and the cost of raw materials per pound is $11.60