Given the graph shows the function:
y(x)
Let's use the graph to estimate y'(a) at different locations.
Using the given graph, we can see the line shows a negative slope.
Apply the slope-intercept form equation with a negative slope:
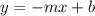
Where:
m and b represent the slope and y-intercepts respectively which are constants.
Now, to find y', let's find the derivative d/dx:
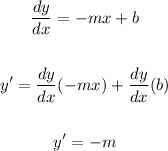
This means the line will be a horizontal line on the negative side of the y-axis.
Therefore, the graph which shows y'(x) is:
ANSWER: