Question

The parent function is f(x) = 2x+4+2 and the new function is g(x) = 2x−1+6.How does the graph change from f(x) to g(x)?Select each correct answer.Question 18 options:The graph is shifted 5 units right.The graph is shifted 4 unit up.The graph is shifted 5 units left.The graph is shifted 4 unit down

Answer 1

We have the function f

`f(x)=2^(x+4)+2`

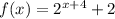
And the function g

`g(x)=2^(x-1)+6`

We can see two major differences, one is in the exponent and one in the constant term, but before talking about them, let's see how operations change the graph, consider a function h(x):

• h(x) + c, shift the graph of h(x) ,up ,"c" units

,

• h(x) - c, shift the graph of h(x) ,down, "c" units

,

• h(x + a), shift the graph of h(x) ,left ,"a" units

,

• h(x - a), shift the graph of h(x) ,right, "a" units

Then, we want to find out the relations between f and g.

Looking at the exponent we can see that the exponent of g is the exponent of f but subtracted 5, see that

`(x+4)-5=x-1`

And on the constant term, we have a difference of 4 positive, then we must add 4 to the function f to get g

Putting that all together, look that

`\begin{gathered} f(x-5)+4=g(x)_{} \\ \\ 2^((x-5)+4)+2+4=2^(x-1)+6 \end{gathered}`

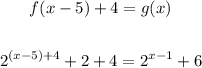
Then, the function g is just f shifted 5 units to the right, and 4 units up