Question

What is the exponential equation that models the population of the city Laredo?Laredo that had a population of 12,600 in 2000.By the year 2006 the population grew to 13,542.(write your equation for p in terms of n . round your b value to 4 decimal places)Use your equation to predict the population in the year 2015The population of Laredo in 2015 should beIn what year will the population reach 28,000 ?

Answer 1

Exponential growth formula

`p=a\cdot b^n`

where

• p: population in year n

,

• a: initial population

,

• b: growth factor (must be greater than 1)

,

• n: time, in years

Taking the year 2000 as n = 0, then initial population is a = 12,600.

In year 2006, n = 6 and p = 13,542. Substituting these values and solving for b:

`\begin{gathered} 13542=12600\cdot b^6 \\ (13542)/(12600)=b^6 \\ \log _(10)((13542)/(12600))=6\cdot\log _(10)b \\ (\log _(10)((13542)/(12600)))/(6)=\log _(10)b \\ 10^(0.0052)\approx b \\ 1.0121\approx b \end{gathered}`

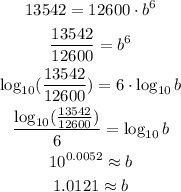
In year 2015, n = 15, therefore

`\begin{gathered} p=12600\cdot1.0121^(15) \\ p\approx15091 \end{gathered}`

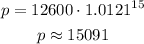
The population of Laredo in 2015 should be approximately 15,091

Substituting p = 28,000 into the equation and solving for n:

`\begin{gathered} 28000=12600\cdot1.0121^n \\ (28000)/(12600)=1.0121^n \\ \log _(10)((28000)/(12600))=n\cdot\log _(10)1.0121 \\ (\log _(10)((28000)/(12600)))/(\log _(10)1.0121)=n \\ 67\approx n \end{gathered}`

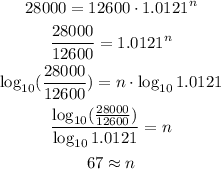
The population will reach 28,000 in 2067 (=2000+67)