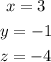Given: A system of linear equations in three variables x, y, and z as follows-
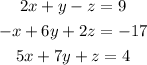
Required: To solve the system using elimination.
Explanation: Let the given system as-
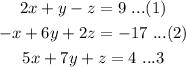
We can solve the system by reducing the system to a system of 2 variables. Suppose we would like to remove the variable z.
Multiplying equation (1) by 2, adding to equation (2) as follows-
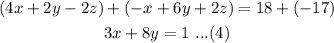
Now, add equations (1) and (3) as follows-
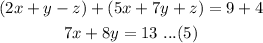
Now, equations (4) and (5) represent a system of linear equations in two variables. Subtracting the equations as follows-
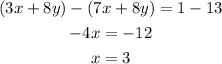
Substituting x=3 in equation (4)-

Substituting x=3 and y=-1 in equation (1) as follows-
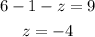
Final Answer: The solution to the system is-