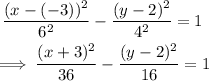Question

I need this problem answered*answer the problem by using the answer options below in the picture*

Answer 1

`\frac{(x+3)^2}{36^{}}-((y-2)^2)/(16)=1`

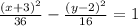
Step-by-step explanation:

The standard form of the equation of a hyperbola with center (h,k) and transverse axis parallel to the x-axis is:

`((x-h)^2)/(a^2)-((y-k)^2)/(b^2)=1`

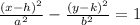
Where:

• The length of the transverse axis = 2a

,

• The length of the conjugate axis = 2b

`\begin{gathered} \text{Centre,}(h,k)=(-3,2) \\ \text{The length of the transverse axis, 2a = 12 units}\implies a=(12)/(2)=6 \\ \text{The length of the conjugate axis, 2b = 8 units}\implies b=(8)/(2)=4 \end{gathered}`

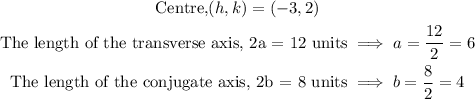
Therefore. the equation of the hyperbola is:

`\begin{gathered} ((x-(-3))^2)/(6^2)-((y-2)^2)/(4^2)=1 \\ \implies\frac{(x+3)^2}{36^{}}-((y-2)^2)/(16)=1 \end{gathered}`