Answer
When x = -1.5, y = 5.25
When y = 5, x = -1.62 and 0.62
(i) (-0.5, 6.25)
(ii) x = -0.5
Step-by-step explanation
From the graph:
When x = -1.5, y = 5.25 (Traced on the graph with red color)
When y = 5, x = -1.62 and 0.62 (Traced on the graph with blue color)
(i) The coordinates of the maximum turning point on the graph is: (-0.5, 6.25) (Traced on the graph with green color).
(ii) To use the formula = -b/2a to justify the x-value at the turning point, we use:
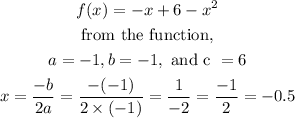
The turning point is justified.