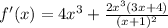We are given the function:
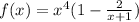
To find its derivative, we can distribute x^4 first so that we won't have to apply both the product rule and the quotient rule.
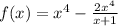
So we'll just solve for the derivative of the first term, x^4, then add it to the derivative of the second term, 2x^4/(x+1).
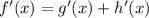
where g(x) = x^4 and h(x) = 2x^4/(x+1).
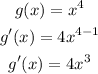
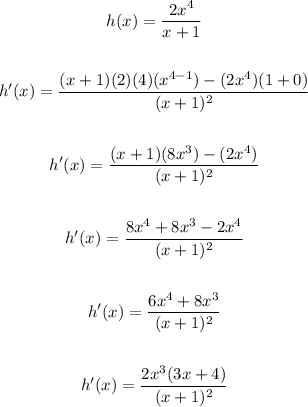
So f'(x) must be: