Question

7. A bullet is fired from the ground making an angle of 30 degwith the horizontal with a speed of 900 m/s.How long it will take to reach its maximum height? (1 point)A. 064.19 sB. O 79.372 sC. 045.918 sD. O 12.353 sIE. O 58.456 s8. A bullet is fired from the ground making an angle of 20 degwith the horizontal with a speed of 1500 m/s.Calculate the maximum height reached? (1 point)A. O 20831.097 m

Answer 1

We will have the following:

First, we determine the middle point of the projectile travel:

`R=((900m/s)^2sin(2\ast30))/(9.8m/s^2)\Rightarrow R=71579.65072...m`

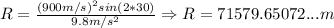
So, the middle point will be approximately half of that, then the time will be determined as follows:

`\begin{gathered} ((900)^2sin(60))/(9.8\ast2)=900cos(30)t+(1)/(2)(0)t^2\Rightarrow900cos(30)t=((900)^2sin(60))/(9.8\ast2) \\ \\ \Rightarrow t=((900)^2sin(60))/(900cos(30)(9.8)(2))\Rightarrow t=(900sin(60))/((9.8)(2)cos(30)) \\ \\ \Rightarrow t=(2250)/(49)s \end{gathered}`

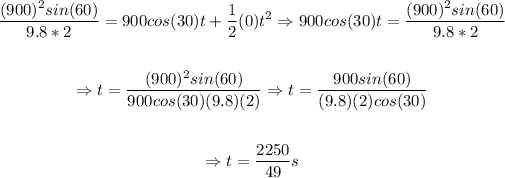
So, the time it will take to reach the maximum height is approximately 45.918s.