When the measure of an angle exceeds 2pi we will subtract 2pi from it to make it less than 2pi
Since the given angle is 11/2 pi, then we will subtract 2pi from it to make it less than 2pi
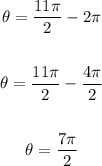
It is still greater than 2 pi, then we will subtract another 2pi
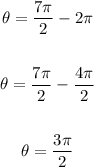
Now, it is less than 2pi, then we will find its sine and cosine

The answer is:
sin(theta) = -1
cos(theta) = 0