Question

how many ways can a male and female be selected to decorate for a party from a club consisting of eight members where five are men and three are women?

Answer 1

The solution to this is to find all possible combinations of male and female to form a team to decorate the party. Of all in attendance, there are 5 males and 3 females. Therefore the team shall consist of;

`\begin{gathered} nC_r=(n!)/(r!(n-r)!) \\ \text{Where n is the number of males/females and } \\ r\text{ is the number to be chosen from the total of each category} \\ For\text{ the males;} \\ 5C_1=(5!)/(1!(5-1)!) \\ 5C_1=(5*4*3*2*1)/(1*(4*3*2*1)) \\ 5C_1=(120)/(1*24) \\ 5C_1=5 \\ \text{For the females;} \\ 3C_1=(3!)/(1!*(3-1)!) \\ 3C_1=(3*2*1)/(1*(2*1)) \\ 3C_1=(6)/(2) \\ 3C_1=3 \\ \text{Therefore;} \\ 5C_1*3C_1=5*3 \\ 5C_1*3C_1=15 \end{gathered}`

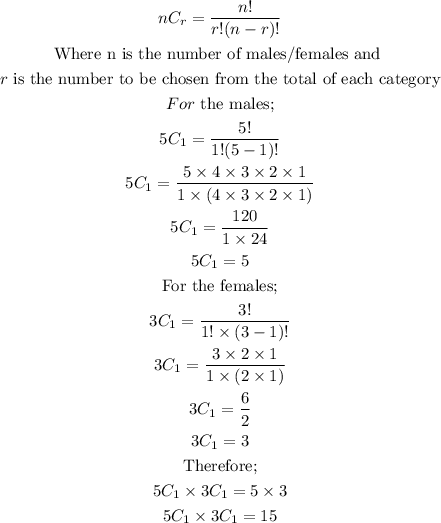
The results shows that they can be selected in 15 different ways