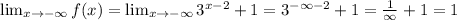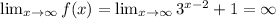Given:
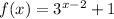
To find:
We need to find the domain, range, asymptotes, and end behavior of the function.
Step-by-step explanation:
Set x=-4 and substitute in the given function.
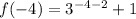
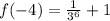
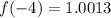
We get the point (-4, 1.001).
Set x=-2 and substitute in the given function.
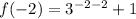

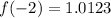
We get the point (-2, 1.0123).
Set x=0 and substitute in the give function.
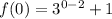
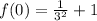
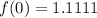
We get (0,1.1111).
Set x=2 and substitute in the give function.

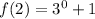
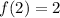
We get the point (2,2).
Mark the points (-4,1.001), (-2,1.012), (0,1.111) and (2,2) on the graph and join points by curve.
The graph of the function is
Recall that the domain of the function is the set of all inputs of the function.
The given function satisfies all values of the real values of x.
Domain:
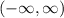
Recall that the range of the function is the set of all output values.
The minimum value of y is 1 and the maximum value is infinity as the function moves upward.
Range:
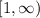
The given function is of the form
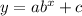
where a=1, b=3 and c=1.
Recall that the exponential function always has the horizontal asymptotes and the equation is y=c.
The asymptotes:
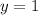
End behavior: