There is an equation for getting the sum of a sequence but there are variables we first need to find.
Sn = (n/2)(2a + (n-1)d)
STEP 1
Getting variables.
Sn = Sum to a the nth ordinal.
n is an arbitrary number
a = first term
d = common difference = Tn - Tn-1 where Tn is the nth term
STEP 2
We substitute into the equation where
n = 23
a = 9
d = 14 - 9 = 19 - 14 = 24 - 19 = 5
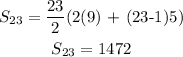
Therefore, the sum of the first 23 terms of the progression is 1472. Option B