Answer:
65.79 sq units
Step-by-step explanation:
We are given this:
Sides of triangle = 8 units
Interior angle between the sides = 72.6 degrees
The sum of the interior angles in a triangle is 180 degrees:
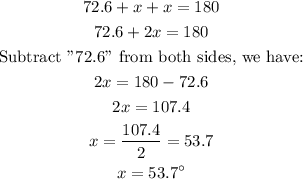
We will obtain the value for the base of the triangle using the Sine rule, we have:
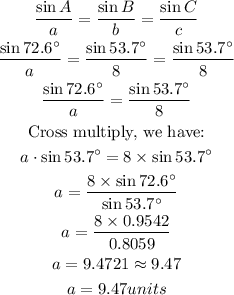
The base of the triangle is 9.47 units
We will thus find the area of the figure as shown below:
![\begin{gathered} Area=Area_(triangle)+Area_(semi-circle) \\ \text{ We will use Heron's formula to calculate the area of the triangle:} \\ Area_(triangle)=\sqrt[]{s(s-a)(s-b)(s-c)} \\ s=(a+b+c)/(2)=(8+8+9.47)/(2)=12.7360\approx12.74 \\ Area_(triangle)=\sqrt[]{12.74(12.74-9.47)(12.74-8)\mleft(12.74-8\mright)} \\ Area_(triangle)=\sqrt[]{12.74(3.27)(4.74)(4.74)} \\ Area_(triangle)=\sqrt[]{935.99572248} \\ Area_(triangle)=30.5940\approx30.59 \\ \\ Area_(semi-circle)=(1)/(2)\pi r^2 \\ Area_(semi-circle)=(1)/(2)*3.14*4.735^2 \\ Area_(semi-circle)=35.19975\approx35.20 \\ Area_(semi-circle)=35.20 \\ \\ Area=30.59+35.20=65.79 \\ \therefore Area=65.79units^2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/41nxtpe5bsnkv3dr647lldgsioc30l7r1b.png)
Therefore, the area of the shape is 65.79 sq units