Question

15#Suppose that pulse rates among healthy adults are normally distributed with a mean of 79 beats/minute and a standard deviation of 10 beats/minute. What proportion of healthy adults have pulse rates that are at most 60 beats/minute? Round your answer to at least four decimal places.

Answer 1

0.0287

Explanation

Z-score formula

`z=(x-\mu)/(\sigma)`

where:

• x: value of interest

,

• μ: mean

,

• σ: standard deviation

In this case, the value of interest is x = 60 beats/minute, the mean is μ = 79 beats/minute, and the standard deviation is σ = 10 beats/minute. Then,

`\begin{gathered} z=(60-79)/(10) \\ z=-1.9 \end{gathered}`

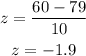
Finding the proportion of healthy adults who have pulse rates that are at most 60 beats/minute is equivalent to finding the next probability:

`P(z\leqslant-1.9)`

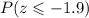
We can find this probability from the following table:

From the table:

`P(z\leqslant-1.9)=0.0287`

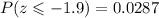
That is, 0.0287 of healthy adults have pulse rates that are at most 60 beats/minute.