1) We write the number that we want to find as:
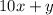
Where x is the tens digit, and y is the unit digit.
2) Its reversed number is:
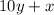
3) The sum of the number and its reverse is equal to 154:
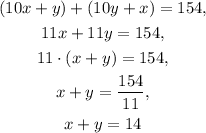
4) One of the digits in the number is 2 less than the tens digit, so we have:
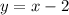
Replacing this in the previous equation that we found and solving for x:
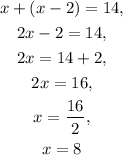
So:
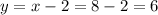
The number that we were looking for is:
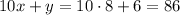
Verification:
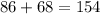
Answer: 86