Question

A. Write an equation representing your shopping experience and use X for the number of candy bars. B. Solve the equation to determine how many candy bars can you purchase? C. How much change would you have left?

Answer 1

a) You have $25 to spend.

The shopping list consists on:

2 gallons of milk for $3.50 each

2 loaves of bread for $2.75

1 pot of roast for $10.45 each

With the remaining money, you want to buy candy bars, which cost $0.43 each.

Let "x" represent the number of candy bars you can buy.

You know that you can spend a maximum of $25 dollars.

First, calculate how much you will spend on the items on the list, to do so, multiply the number of units you have to buy for each item by their cost and add the results:

`(2*3.50)+(2*2.75)+(1*10.45)=7+5.50+10.45=22.95`

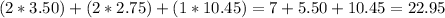
Next, to write the equation, you have to express how much you will spend on "x" candy bars by multiplying the cost per candy bar by x: 0.43x

If you add the money spent on the items on the list and the money spent on the candy bars, the result must be no more than $25, so that:

`22.95+0.43x\leq25`

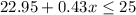
b) Using the equation above, you can calculate how many candy bars you can buy by solving the inequation for x:

`\begin{gathered} 22.95+0.43x\leq25→subtract\text{ }22.95\text{ }to\text{ }both\text{ }sides \\ 22.95-22.95+0.43x\leq25-22.95 \\ 0.43x\leq2.05→divide\text{ }by\text{ }0.43 \\ (0.43)/(0.43)x\leq(2.05)/(0.43) \\ x\leq4.77 \end{gathered}`

The number of candy bars you can buy is equal to the whole number of the value obtained for x. So, you can buy 4 candy bars.

c) To determine how much money is remaining, you have to add the amount spent on the items on the list and the amount spent on the candy bars and subtract it from the initial $25.

- Add the amounts spent

`22.95+4*0.43=22.95+1.72=24.67`

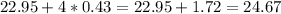
-Subtract the result to the initial amount of money

`25-24.67=0.33`

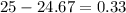
After the purchase, you will have 33 cents left.