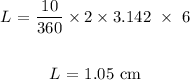Answer:

Step-by-step explanation:
a) Here, we want to get the length of the arc
Mathematically, we can calculate that using the formula:
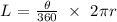
where r is the radius of the circle which is 5 cm
theta is the central angle subtended by the arc which is 10 degrees
Substituting the values, we have it that:
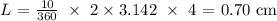
b) The arc will be shorter than the one on a circle with a radius of 6 cm
The reason for this is that a circle with a radius of 6 cm will be larger than one with a radius of 4 cm
c) Here, we want to find the length if the radius was 6 cm
We simply substitute for the radius and the central angle as we have done in (a)
We have that as: