We solve as follows:
Since we have:
![\lim _(\theta\rightarrow0)\frac{2\sin (\sqrt[]{2}\theta)}{\sqrt[]{2}\theta}](https://img.qammunity.org/2023/formulas/mathematics/college/scft9dheg0sthyxokveu8qbbv79dh1564m.png)
We can proceed as follows:
We assign a new denomination:
![\alpha=\sqrt[]{2}\theta](https://img.qammunity.org/2023/formulas/mathematics/college/499xgo3k5o4qrs4l78l2549gi5bq6cvdi2.png)
And we solve for theta = 0:
![\alpha=\sqrt[]{2}(0)\Rightarrow\alpha=0](https://img.qammunity.org/2023/formulas/mathematics/college/22ci7d539w8lk3xyzokffyo1w6vaspgm7y.png)
Now, we re-write the original expression:
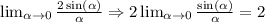
And, since we already know the following:
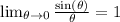
Then, we will have that the solution will be:
![\lim _(\theta\rightarrow0)\frac{2\sin (\sqrt[]{2}\theta)}{\sqrt[]{2}\theta}=2](https://img.qammunity.org/2023/formulas/mathematics/college/lj47ctc350ljppzws0ds157i53uqolybza.png)