We have the next quadratic equation
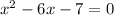
in order to have a trinomial perfect square that is
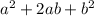
in this case, we have
a= x
b= -3
so the expected value
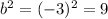
In order to complete the square, we need to add the number 9 on both sides of the equation
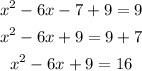
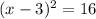
Because we have a quadratic equation we will have 2 solutions for x
![\begin{gathered} (x-3)=\pm\sqrt[]{16} \\ x-3=\pm4 \\ x_1=4+3=7 \\ x_2=-4+3=-1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/fde4aqh418y8b13x004b06kz624gwugwde.png)
the solution is
x1=7
x2=-1