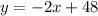Question

In the coordinate plane below. triangle DEF is similar to triangle HIJ.

Answer 1

Part A

we can calculate the slope taking two points of the line and using the slope formula

`m=(y2-y1)/(x2-x1)`

where (x2,y2) is a right point from (x1,y1)

i will use the points (8,32) and (12,24)

so replacing

`\begin{gathered} m=(24-32)/(12-8) \\ \\ m=(-8)/(4)=-2 \end{gathered}`

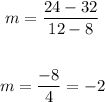
the slope is -2

Part B

to make the equation we use the general form of the line

`y=mx+b`

where m is the slope and b the y-intercept, we have the slope because s is the same line than HI

so m=-2

now replace the slope and a point on the general equation to find b

i will use the point (8,32)

`\begin{gathered} (32)=(-2)(8)+b \\ 32=-16+b \\ b=32+16 \\ b=48 \end{gathered}`

now we can rewrite the equation replacing b=48 and m=-2

the equation is

`y=-2x+48`