For item a) we need to find the maxima of a function. If we take the derivative of a function, when its equal to 0, it could be a maxima or a minima
Let's take the derivative:
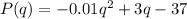
By using the derivative rules:
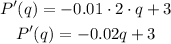
Now, by making the derivative equal 0, we can find the critic points:
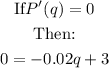
And solve for q:
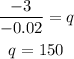
We can infer that the function P(q) has a critical point in q = 150. To know what is the nature of that critical point, we can take the second derivative:

Since the second derivative is negative, the point q = 150 is a maximum.
Thus, the answer to question a is
Answer: 150 thousand pairs of sunglasses needs to be sold.
Now to part b)
Since the maximum profit will occur when q = 150, to know the maximum profit, we need to evaluate P(q) when q = 150:

Solving:
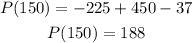
The answer to b is:
Answer: 188 thousand dollars of maximum profit can be expected