Solution:
Let H represent the height.
Given that the initial height from which the rubber ball is dropped is 800 centimeters, this implies that
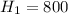
It is noticed that after each bounce, it reached 85% of its previous height. This implies that
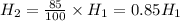
Similarly,

Thus, since each height is attained by a common ratio, using the geometric sequence formula expressed as

Thus, substituting these parameters into the geometric sequence formula, we have
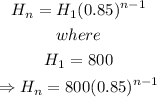
Hence, the equation model for the height H, for n bounces is

The third option is the correct answer.